Group A4

• Generators:g1=g1, g2a=g2a, g2b=g2b
• Representations:dim3, dim1a, dim1b.
• Conjugacy Class 1 of Group A4 Graph1 - 3 elements in conjugacy class including Example1_1

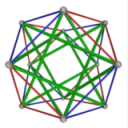
  Cable 1:[4, 2, 1, 3].

  Orders of Disjoint Cycles: [3].

  Cable 2:[1, 4, 2, 3].

  Orders of Disjoint Cycles: [3].

• Conjugacy Class 2 of Group A4 Graph2 - 3 elements in conjugacy class including Example2_1

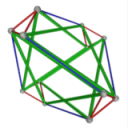
  Cable 1:[2, 4, 3, 1].

  Orders of Disjoint Cycles: [3].

  Cable 2:[4, 3, 2, 1].

  Orders of Disjoint Cycles: [2, 2].

Group S4

• Generators:g1=[2, 1, 3, 4], g2=[2, 3, 1, 4], g3=[2, 3, 4, 1]
• Representations:dim1, dim2, dim3a, dim3b.
• Conjugacy Class 1 of Group S4 Graph1 - 9 elements in conjugacy class including Example1_1

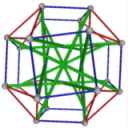
  Cable 1:[4, 3, 1, 2].

  Orders of Disjoint Cycles: [4].

  Cable 2:[1, 4, 2, 3].

  Orders of Disjoint Cycles: [3].

• Conjugacy Class 2 of Group S4 Graph2 - 9 elements in conjugacy class including Example2_1

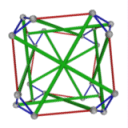
  Cable 1:[2, 1, 3, 4].

  Orders of Disjoint Cycles: [2].

  Cable 2:[4, 2, 1, 3].

  Orders of Disjoint Cycles: [3].

• Conjugacy Class 3 of Group S4 Graph3 - 10 elements in conjugacy class including Example3_1

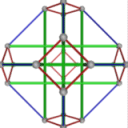
  Cable 1:[3, 2, 1, 4].

  Orders of Disjoint Cycles: [2].

  Cable 2:[4, 3, 1, 2].

  Orders of Disjoint Cycles: [4].

• Conjugacy Class 4 of Group S4 Graph4 - 6 elements in conjugacy class including Example4_1

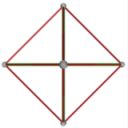
  Cable 1:[3, 1, 4, 2].

  Orders of Disjoint Cycles: [4].

  Cable 2:[4, 3, 1, 2].

  Orders of Disjoint Cycles: [4].

Group A4Z2

• Generators:g1=[2, 3, 1, 4, 5, 6], g2a=[2, 1, 4, 3, 5, 6], g2b=[3, 4, 1, 2, 5, 6], ref=[1, 2, 3, 4, 6, 5]
• Representations:dim3, dim1a, dim1b, dim3r, dim1ar, dim1br.
• Conjugacy Class 1 of Group A4Z2 Graph1 - 9 elements in conjugacy class including Example1_1

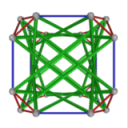
  Cable 1:[3, 4, 1, 2, 6, 5].

  Orders of Disjoint Cycles: [2, 2, 2].

  Cable 2:[2, 4, 3, 1, 5, 6].

  Orders of Disjoint Cycles: [3].

• Conjugacy Class 2 of Group A4Z2 Graph2 - 9 elements in conjugacy class including Example2_1

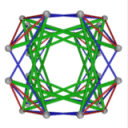
  Cable 1:[4, 2, 1, 3, 6, 5].

  Orders of Disjoint Cycles: [3, 2].

  Cable 2:[2, 4, 3, 1, 5, 6].

  Orders of Disjoint Cycles: [3].

• Conjugacy Class 3 of Group A4Z2 Graph3 - 9 elements in conjugacy class including Example3_1

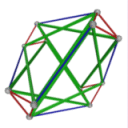
  Cable 1:[1, 3, 4, 2, 6, 5].

  Orders of Disjoint Cycles: [3, 2].

  Cable 2:[2, 1, 4, 3, 5, 6].

  Orders of Disjoint Cycles: [2, 2].

• Conjugacy Class 4 of Group A4Z2 Graph4 - 9 elements in conjugacy class including Example4_1

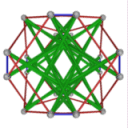
  Cable 1:[1, 3, 4, 2, 6, 5].

  Orders of Disjoint Cycles: [3, 2].

  Cable 2:[2, 1, 4, 3, 6, 5].

  Orders of Disjoint Cycles: [2, 2, 2].

• Conjugacy Class 5 of Group A4Z2 Graph5 - 8 elements in conjugacy class including Example5_1

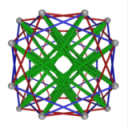
  Cable 1:[1, 3, 4, 2, 6, 5].

  Orders of Disjoint Cycles: [3, 2].

  Cable 2:[4, 2, 1, 3, 6, 5].

  Orders of Disjoint Cycles: [3, 2].

Group S4Z2

• Generators:g1=[2, 1, 3, 4, 5, 6], g2=[2, 3, 1, 4, 5, 6], g3=[2, 3, 4, 1, 5, 6], ref=[1, 2, 3, 4, 6, 5]
• Representations:dim1, dim2, dim3a, dim3b, dim1r, dim2r, dim3ar, dim3br.
• Conjugacy Class 1 of Group S4Z2 Graph1 - 23 elements in conjugacy class including Example1_1

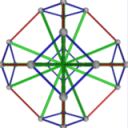
  Cable 1:[2, 4, 1, 3, 6, 5].

  Orders of Disjoint Cycles: [4, 2].

  Cable 2:[1, 2, 4, 3, 5, 6].

  Orders of Disjoint Cycles: [2].

• Conjugacy Class 2 of Group S4Z2 Graph2 - 21 elements in conjugacy class including Example2_1

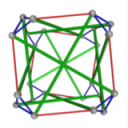
  Cable 1:[2, 3, 1, 4, 6, 5].

  Orders of Disjoint Cycles: [3, 2].

  Cable 2:[4, 2, 3, 1, 6, 5].

  Orders of Disjoint Cycles: [2, 2].

• Conjugacy Class 3 of Group S4Z2 Graph3 - 23 elements in conjugacy class including Example3_1

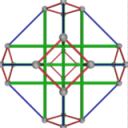
  Cable 1:[4, 2, 3, 1, 6, 5].

  Orders of Disjoint Cycles: [2, 2].

  Cable 2:[4, 1, 2, 3, 5, 6].

  Orders of Disjoint Cycles: [4].

• Conjugacy Class 4 of Group S4Z2 Graph4 - 19 elements in conjugacy class including Example4_1

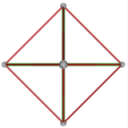
  Cable 1:[3, 4, 2, 1, 6, 5].

  Orders of Disjoint Cycles: [4, 2].

  Cable 2:[4, 1, 2, 3, 5, 6].

  Orders of Disjoint Cycles: [4].

• Conjugacy Class 5 of Group S4Z2 Graph5 - 21 elements in conjugacy class including Example5_3

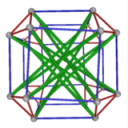
  Cable 1:[3, 4, 2, 1, 6, 5].

  Orders of Disjoint Cycles: [4, 2].

  Cable 2:[4, 1, 3, 2, 6, 5].

  Orders of Disjoint Cycles: [3, 2].

• Conjugacy Class 6 of Group S4Z2 Graph6 - 21 elements in conjugacy class including Example6_1

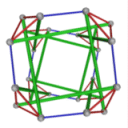
  Cable 1:[2, 3, 1, 4, 6, 5].

  Orders of Disjoint Cycles: [3, 2].

  Cable 2:[4, 2, 3, 1, 5, 6].

  Orders of Disjoint Cycles: [2].

• Conjugacy Class 7 of Group S4Z2 Graph7 - 21 elements in conjugacy class including Example7_1

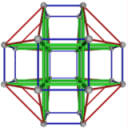
  Cable 1:[4, 3, 1, 2, 5, 6].

  Orders of Disjoint Cycles: [4].

  Cable 2:[2, 3, 1, 4, 6, 5].

  Orders of Disjoint Cycles: [3, 2].

Group A5

• Generators:g1=g1, g2a=g2a, g2b=g2b, g3=g3
• Representations:dim3a, dim3b, dim4, dim5.
• Conjugacy Class 1 of Group A5 Graph1 - 21 elements in conjugacy class including Example1_1

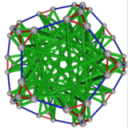
  Cable 1:[4, 2, 1, 3, 5].

  Orders of Disjoint Cycles: [3].

  Cable 2:[1, 3, 2, 5, 4].

  Orders of Disjoint Cycles: [2, 2].

• Conjugacy Class 2 of Group A5 Graph2 - 21 elements in conjugacy class including Example2_1

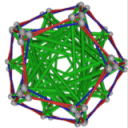
  Cable 1:[2, 3, 5, 1, 4].

  Orders of Disjoint Cycles: [5].

  Cable 2:[5, 4, 3, 2, 1].

  Orders of Disjoint Cycles: [2, 2].

• Conjugacy Class 3 of Group A5 Graph3 - 21 elements in conjugacy class including Example3_1

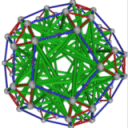
  Cable 1:[4, 2, 1, 3, 5].

  Orders of Disjoint Cycles: [3].

  Cable 2:[2, 3, 5, 1, 4].

  Orders of Disjoint Cycles: [5].

• Conjugacy Class 4 of Group A5 Graph4 - 21 elements in conjugacy class including Example4_1

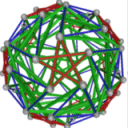
  Cable 1:[5, 2, 3, 1, 4].

  Orders of Disjoint Cycles: [3].

  Cable 2:[2, 3, 5, 1, 4].

  Orders of Disjoint Cycles: [5].

• Conjugacy Class 5 of Group A5 Graph5 - 14 elements in conjugacy class including Example5_1

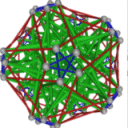
  Cable 1:[4, 3, 5, 2, 1].

  Orders of Disjoint Cycles: [5].

  Cable 2:[2, 3, 5, 1, 4].

  Orders of Disjoint Cycles: [5].

• Conjugacy Class 6 of Group A5 Graph6 - 21 elements in conjugacy class including Example6_1

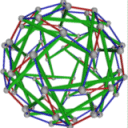
  Cable 1:[5, 4, 1, 3, 2].

  Orders of Disjoint Cycles: [5].

  Cable 2:[5, 2, 4, 3, 1].

  Orders of Disjoint Cycles: [2, 2].

• Conjugacy Class 7 of Group A5 Graph7 - 9 elements in conjugacy class including Example7_1

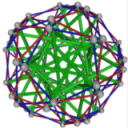
  Cable 1:[4, 1, 3, 2, 5].

  Orders of Disjoint Cycles: [3].

  Cable 2:[1, 2, 5, 3, 4].

  Orders of Disjoint Cycles: [3].

• Conjugacy Class 8 of Group A5 Graph8 - 15 elements in conjugacy class including Example8_1

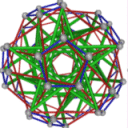
  Cable 1:[4, 5, 1, 2, 3].

  Orders of Disjoint Cycles: [5].

  Cable 2:[4, 5, 2, 3, 1].

  Orders of Disjoint Cycles: [5].

Group A5Z2

• Generators:g1=[2, 3, 1, 4, 5, 6, 7], g2a=[2, 1, 4, 3, 5, 6, 7], g2b=[3, 4, 1, 2, 5, 6, 7], g3=[2, 3, 4, 5, 1, 6, 7], ref=[1, 2, 3, 4, 5, 7, 6]
• Representations:dim3a, dim3b, dim4, dim5, dim3ar, dim3br, dim4r, dim5r.
• Conjugacy Class 1 of Group A5Z2 Graph1 - 10 examples without vertex overlap including Example1_2

  Cable 1:[1, 3, 2, 5, 4, 6, 7].

  Orders of Disjoint Cycles: [2, 2].

  Cable 2:[3, 5, 4, 2, 1, 7, 6].

  Orders of Disjoint Cycles: [5, 2].

• Conjugacy Class 2 of Group A5Z2 Graph2 - 1 example without vertex overlap including Example2_16

  Cable 1:[5, 1, 3, 4, 2, 7, 6].

  Orders of Disjoint Cycles: [3, 2].

  Cable 2:[1, 3, 2, 5, 4, 6, 7].

  Orders of Disjoint Cycles: [2, 2].

• Conjugacy Class 3 of Group A5Z2 Graph3 - 10 examples without vertex overlap including Example3_1

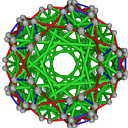
  Cable 1:[3, 5, 4, 2, 1, 7, 6].

  Orders of Disjoint Cycles: [5, 2].

  Cable 2:[1, 3, 2, 5, 4, 7, 6].

  Orders of Disjoint Cycles: [2, 2, 2].

• Conjugacy Class 4 of Group A5Z2 Graph4 - 11 examples without vertex overlap including Example4_3

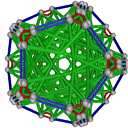
  Cable 1:[2, 4, 3, 1, 5, 6, 7].

  Orders of Disjoint Cycles: [3].

  Cable 2:[1, 3, 2, 5, 4, 7, 6].

  Orders of Disjoint Cycles: [2, 2, 2].

• Conjugacy Class 5 of Group A5Z2 Graph5 - 18 examples without vertex overlap including Example5_3

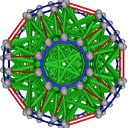
  Cable 1:[2, 4, 5, 3, 1, 6, 7].

  Orders of Disjoint Cycles: [5].

  Cable 2:[1, 3, 2, 5, 4, 7, 6].

  Orders of Disjoint Cycles: [2, 2, 2].

• Conjugacy Class 6 of Group A5Z2 Graph6 - 4 examples without vertex overlap including Example6_1

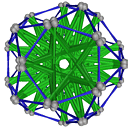
  Cable 1:[3, 4, 2, 5, 1, 7, 6].

  Orders of Disjoint Cycles: [5, 2].

  Cable 2:[1, 3, 2, 5, 4, 7, 6].

  Orders of Disjoint Cycles: [2, 2, 2].

• Conjugacy Class 7 of Group A5Z2 Graph7 - 1 example without vertex overlap including Example7_10

  Cable 1:[4, 3, 1, 5, 2, 7, 6].

  Orders of Disjoint Cycles: [5, 2].

  Cable 2:[1, 3, 2, 5, 4, 6, 7].

  Orders of Disjoint Cycles: [2, 2].

• Conjugacy Class 8 of Group A5Z2 Graph8 - 2 examples without vertex overlap including Example8_25

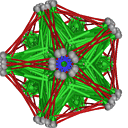
  Cable 1:[3, 5, 4, 2, 1, 6, 7].

  Orders of Disjoint Cycles: [5].

  Cable 2:[2, 4, 3, 1, 5, 7, 6].

  Orders of Disjoint Cycles: [3, 2].

• Conjugacy Class 9 of Group A5Z2 Graph9 - 5 examples without vertex overlap including Example9_7

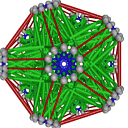
  Cable 1:[3, 4, 5, 1, 2, 6, 7].

  Orders of Disjoint Cycles: [5].

  Cable 2:[4, 5, 3, 1, 2, 7, 6].

  Orders of Disjoint Cycles: [2, 2, 2].

• Conjugacy Class 10 of Group A5Z2 Graph10 - 0 examples without vertex overlap.

  Cable 1:[4, 2, 3, 5, 1, 7, 6].

  Orders of Disjoint Cycles: [3, 2].

  Cable 2:[3, 1, 2, 4, 5, 7, 6].

  Orders of Disjoint Cycles: [3, 2].

• Conjugacy Class 11 of Group A5Z2 Graph11 - 5 examples without vertex overlap including Example11_2

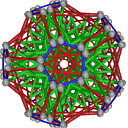
  Cable 1:[2, 3, 5, 1, 4, 6, 7].

  Orders of Disjoint Cycles: [5].

  Cable 2:[3, 1, 2, 4, 5, 7, 6].

  Orders of Disjoint Cycles: [3, 2].

• Conjugacy Class 12 of Group A5Z2 Graph12 - 1 example without vertex overlap including Example12_30

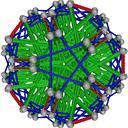
  Cable 1:[1, 5, 4, 3, 2, 7, 6].

  Orders of Disjoint Cycles: [2, 2, 2].

  Cable 2:[3, 1, 2, 4, 5, 7, 6].

  Orders of Disjoint Cycles: [3, 2].

• Conjugacy Class 13 of Group A5Z2 Graph13 - 2 examples without vertex overlap including Example13_8

  Cable 1:[3, 1, 2, 4, 5, 7, 6].

  Orders of Disjoint Cycles: [3, 2].

  Cable 2:[1, 2, 4, 5, 3, 6, 7].

  Orders of Disjoint Cycles: [3].

• Conjugacy Class 14 of Group A5Z2 Graph14 - 2 examples without vertex overlap including Example14_7

  Cable 1:[3, 1, 2, 4, 5, 7, 6].

  Orders of Disjoint Cycles: [3, 2].

  Cable 2:[3, 1, 4, 5, 2, 7, 6].

  Orders of Disjoint Cycles: [5, 2].

• Conjugacy Class 15 of Group A5Z2 Graph15 - 10 examples without vertex overlap including Example15_3

  Cable 1:[2, 4, 5, 3, 1, 7, 6].

  Orders of Disjoint Cycles: [5, 2].

  Cable 2:[3, 2, 5, 4, 1, 6, 7].

  Orders of Disjoint Cycles: [3].

• Conjugacy Class 16 of Group A5Z2 Graph16 - 1 example without vertex overlap including Example16_8

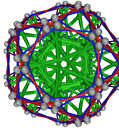
  Cable 1:[2, 4, 5, 3, 1, 7, 6].

  Orders of Disjoint Cycles: [5, 2].

  Cable 2:[4, 5, 1, 2, 3, 7, 6].

  Orders of Disjoint Cycles: [5, 2].

• Conjugacy Class 17 of Group A5Z2 Graph17 - 2 examples without vertex overlap including Example17_19

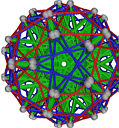
  Cable 1:[5, 1, 3, 4, 2, 7, 6].

  Orders of Disjoint Cycles: [3, 2].

  Cable 2:[4, 5, 1, 2, 3, 7, 6].

  Orders of Disjoint Cycles: [5, 2].

• Conjugacy Class 18 of Group A5Z2 Graph18 - 16 examples without vertex overlap including Example18_2

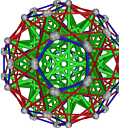
  Cable 1:[3, 5, 2, 1, 4, 6, 7].

  Orders of Disjoint Cycles: [5].

  Cable 2:[4, 5, 1, 2, 3, 7, 6].

  Orders of Disjoint Cycles: [5, 2].

• Conjugacy Class 19 of Group A5Z2 Graph19 - 8 examples without vertex overlap including Example19_1

  Cable 1:[3, 5, 4, 2, 1, 7, 6].

  Orders of Disjoint Cycles: [5, 2].

  Cable 2:[4, 5, 1, 2, 3, 7, 6].

  Orders of Disjoint Cycles: [5, 2].

• Conjugacy Class 20 of Group A5Z2 Graph20 - 10 examples without vertex overlap including Example20_2

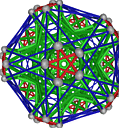
  Cable 1:[2, 4, 5, 3, 1, 6, 7].

  Orders of Disjoint Cycles: [5].

  Cable 2:[4, 5, 1, 2, 3, 7, 6].

  Orders of Disjoint Cycles: [5, 2].

• Conjugacy Class 21 of Group A5Z2 Graph21 - 7 examples without vertex overlap including Example21_2

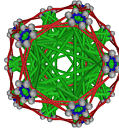
  Cable 1:[1, 5, 2, 4, 3, 6, 7].

  Orders of Disjoint Cycles: [3].

  Cable 2:[2, 4, 5, 3, 1, 7, 6].

  Orders of Disjoint Cycles: [5, 2].