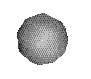Catalogue of Symmetric Tensegrities

by Allen Back and Bob Connelly

Introduction

This is an in progress

catalogue

of descriptions and computer genenerated pictures of certain structures called tensegrities that have a very specific sense of symmetry. They are built with the following.

Cables denoted by: or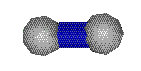

The ends of the cables are allowed to get closer together or stay the same length but not further apart. They are always colored red or blue.

Struts denoted by: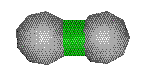

The ends of the struts are allowed to get further apart or stay the same length but not closer together. They are always colored green.

They are joined at their ends by

Vertices denoted by: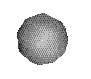

Vertices are points in space that are constrained to satisfy the cable and strut conditions.

For more information, discussion and pictures, see our article Symmetric Tensegrities in the March-April 1998 issue of the American Scientist.

Stability

One use of this catalogue is to find examples of tensegrities that will hold their shape when sticks (or dowels, say) are used for the struts and string (or cord) is used for the cables.

We will be mostly concerned with a particular condition called super stability, that implies that the structure will hold its shape in a very strong sense. For example, it is usually possible to use rubber bands instead of string or cord, and the structure will still hold its shape quite well.

Catalogue Information

In the catalogue, usually a picture appears only if it represents a super stable configuration. But there are some exceptions when the description says that there is a "Possible Tie". This means that the structure is probably rigid, but that there may be some other non-congruent configurations with the same cable and strut lengths.

Combinatorially, we view this class of symmetric tensegrities as having one vertex for each element of the underlying group G and 3 combinatorially distinct basic edges (or edge pairs, really) coming out of the basepoint vertex. However because of the way that the group is represented as transformations of a Euclidean space, it can sometimes turn out that combinatorially distinct vertices and edges actually coincide.

Hence other qualifiers which appear annotating some examples are the phrases:

• Vertex Overlap reporting how many (when more than 1) combinatorially distinct vertices in the example coincide with a reference basepoint vertex.
• Edge Overlap reporting how many (when more than 1) edges in the example coincide with combinatorially distinct edges at the basepoint vertex.
• Degenerate Edges reporting how many (when more than 1) basic edges at the basepoint have length 0.

Each example is also annotated with a minimum strut stress -w1_min. Our technique for proving superstability involves the symmetric assignment of a stress (like a spring constant) to each member. Although the theory is more general, the pictures here at the moment have a stress of +1 on each cable and the stress -w1_min on each strut.

We refer to the representation with this minimum -w1_min value as the winning representation. Our basic theorem guarantees the superstability of the associated tensegrity.

The Abstract Symmetry Groups

The catalogue is organized by the type of abstract group of symmetries of the underlying tensegrity. There are six groups that we are concerned with for this catalogue. First we have the following three groups:

• The Alternating Group of even permutations of 4 elements: A₄
• The Symmetric Group of all permutations of 4 elements: S₄
• The Alternating Group of even permutations of 5 elements: A₅

And then with each of these groups one takes the direct sum with the group with 2 elements, Z₂. This gives three more groups:

• A₄ + Z₂
• S₄ + Z₂
• A₅ + Z₂

The theory is such that this is a natural method of classification. But one must realize that for each of these groups, there is more than one representation of that group as a group of symmetries of a Euclidean space. All of them, except A₄, even have different irreducible representations in three-space.

The Underlying Graph and the Fine Classification

The following describes how the classification is perfomed within each abstract symmetry group

The catalogue is further organized first according to the underlying cable graph and then finally according to the full underlying graph of cables AND struts.

After choosing an (arbritrary) vertex as basepoint, all other vertices are labeled combinatorially by the element g of the group taking the basepoint to the given vertex. The basepoint corresponds to the identity e.

Edges which are related by transformations of the symmetry group are colored the same. Combinatorially an edge is described by a pair of group elements labeling its endpoints. By the action of the group, each edge will correspond to one at the identity e. So if [e,g₁] is a member then [e,g₁^-1] will also be one.

Conventionally we use g₁ to indicate the group element describing a strut at the basepoint. Cables at the basepoint are described by group elements g₂ and g₃.

Replacing any of these g_i by their inverses do not change the tensegrity, since the group takes each of these basic edges to the other. So combinatorially, the underlying graph of one of our symmetric tensegrities is described by the 2 element list [{g₁,g₁^-1},{{g₂ ,g₂^-1 },{g₃ ,g₃^-1 }}]. Here {} is used to denote a set, where order of elements is unimportant.

Furthermore, if there is a symmetry of the group (technically an automorphism) which takes one of these triples to another, then combinatorially we have the same tensegrity. Our catalog keeps this in mind and presents only one instance of each such equivalence class.

To be super stable, the two cable group elements must generate the group, so we only consider configurations satisfying this condition.

In the information accompanying the picture of the tensegrity, there is a description of each of these three group elements as a permutation in disjoint cycle notation. So for example, for the group S₄, [[1,2],[3,4]] denotes the permutation that takes 1 to 2, 2 to 1, 3 to 4, and 4 to 3.

Some things to watch out for

For almost all of the examples shown here, once the underlying graph is determined, then there is a one-parameter family of tensegrities, all different up to congruence, even when one of the cable or strut lengths are fixed. For example, one can fix the strut length, and then vary the ratio between the lengths of the red and blue cables. In this catalogue the default configuration is such that if it is possible to have a symmetry between the red and blue cables, that will be the chosen configuration. Sometimes this has the unfortunate side-effect that in those situations, some of the vertices will overlap, while a more generic configuration will separate them. But recall that if the winning configuration is unfaithful, then some of the vertices will overlap, no matter what the ratio between the red and blue cable lengths is. One technique by which can study all possible cable and strut stress ratios systematically by the use of determinant plots.

The Representations of the Abstract Symmetry Groups

Each of the abstract symmetry groups above can be represented as a group of rotations, reflections and compositions of such on Euclidean spaces of various dimensions including three-space. Sometimes there will even be several distinct 3 dimenssional representations.

In a sense, each of these representations "compete" against each other to be the super stable configuration with a given combinatorial type for its underlying graph. If the winner of the competition happens to be a unique three-representation, then we are able show a picture of such a three-dimensional configuration for a super stable tensegrity.

The following is a list, with comments, of the relevant representations for the first three groups above. All the groups have a trivial representation that sends every group element to the identity. We will only describe the others. We will also only describe the irreducible representations, those that cannot be broken down into a sum of other lower dimensional representations. A representation is faithful if each group element corresponds to a distinct symmetry of Euclidean space. If the representation is not faithful, then the tensegrity that corresponds to it will have vertices that lie on top of each other. (This happens quite often for the groups with a Z₂ factor above.)

For each representation, on an auxiliary page, we mention algebraically the matrices associated with that representation on a generating set for the group.

A₄:

• Two one-dimensional unfaithful complex representations which we denote as dim1a and dim1b.
• A three-dimensional faithful representation dim3 consisting of the rotations of the regular tetrahedron.

S₄:

• A one-dimensional adulterous representation dim1 obtained by taking each even permutation to +1 and each odd permutatation to -1.
• A two-dimensional unfaithful representation dim2.
• A three-dimensional faithful representation dim3b that consists of all the symmetries of the regular tetrahedron.
• A three-dimensional faithful representation dim3athat consists of all the rotations of a cube.

A₅:

• Two three-dimensional faithful representations dim3a and dim3b that consists of the rotations of a regular dodecahedron. They are distinquished by the labeling that corresponds to each group element. As sets they are the same.
• A four-dimensional faithful representation dim4 that consists of all the "rotations" of the regular simplex in four-space.
• A five-dimensional faithful representation dim5.

For the other three groups with the extra Z₂ component, there are exactly twice as many representations. For one set of representations, the Z₂ factor is igonred, and all those representations are unfaithful. For the other set of representations, incuding the trivial representation, the Z₂ element is taken into account by multiplying all the coordinates by -1.

[ Department Home | Lab Home ]

Last Update: March 8, 1998