|
The research we did this summer (1999) was to implement the Finite Element
Method on the Sierpinski Gasket. The first thing we want to do is familiarize
you with the Sierpinski Gasket...
So basically, if you take an equilateral triangle and make an upside-down
triangle by connecting the midpoints of each side, and do that until infinity:
you have the Sierpinski Gasket. (As shown in the upper-left hand corner of this screen)
Throughout this site you will find abbreviations
so here is a little table which might help:
| Various Notation
|
| L(u) |
Laplacian of the fn. u |
| Pu |
Approximate solution |
| Vm |
The level of the gasket |
| Um |
The approximate solution on a certain
level
of the gasket |
| Hj |
(j+1)-harmonic fn. |
| S(Hj, Vm) |
The spline space |
The differential equation we are trying to solve is:
-L(u) + q*u = f
We are using a method of splines to find solutions to this
fractal differential eqn using the finite element method. For more information on splines, you can download
the paper "Splines on Fractals" by Bob Strichartz and Mike Usher by
clicking here. Basically, the method
boils down to solving a system of linear equations for the coefficients of a
spline approximation to the function. Also, if you would like to see
Mike Usher's work used for the "Splines on Fractals" paper,
click here.
For our solutions, we used harmonic and biharmonic splines, which are the
analogs of piecewise linear and piecewise cubic approximations, respectively.
Basically, by using the bi-harmonic splines, we get the advantage of being
able to control the first derivative as well as the value of the function,
which yields a better approximation (like taking another term in a Taylor
series).
Now if you are curious as to what a harmonic function looks like, look below:
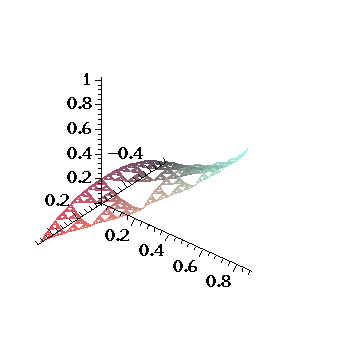
All of our prodedures, programs, code, etc you will find on the page
titled "Lots of Programs." The code is thoroughly documented and there
is also an outline which we think will help you understand the code. If you have
maple, you can download the code, and we provide sample worksheets which will allow you
to get information on functions of your choice. So enjoy the rest of the site.
There has been work done on the Sierpinski Gasket in the past; one site that
might interest you, or give you more background information is the site by Kyallee Dalrymple.
| 



