> read(`c:/othermaple/plot3d_region02.txt`);
Warning, the name changecoords has been redefined
Warning, the name arrow has been redefined
![]()
> help_plot3d_region();
EXAMPLE: > gr0:=plot3d_region(x=-1..1,y=-sqrt(1-x^2)..sqrt(1-x^2),z=-1+sqrt(x^2+y^2)..sqrt(1-x^2-y^2));
> display(gr0); display([gr0[1],gr0[2]); display([op(3..6,gr0)]);
to describe an ice cream cone.
The fourth argument (20 in the example) controls coarseness of the picture.
Time and memory requirements can be proportional to the cube of this number.
A list of 6 plot structures is returned.
For all these, one would want to sketch the bounding surfaces and regions before
trying to set up the limits of integration. (The function plot3d_region is really
visualizing the limits supplied, not figuring out the right limits.)
However, to give you a better feel for what we are seeking in setting up a triple
integral, spend a little time thinking at how the solid pictured arises from
the problem specification and the limits supplied.
Remember that in the triple integral
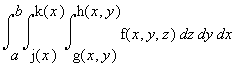 ,
,
1. For fixed values of x and y, the limits g(x,y) and h(x,y) describe the
intersection with the solid of the corresponding line parallel to the z axis.
2. The outer two limits of integration
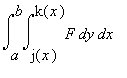 (after the inner z integral is done)
(after the inner z integral is done)
describe the projection of the solid into the xy plane.
Cube. (The Simplest Case.)
Unit Cube 0 <=x <=1,0 <=y<=1,0 <=z <=1.
>
gra:=plot3d_region(x=-1..1,y=-1..1,z=-1..1,11):
display(gra); display([gra[1],gra[2]],title=`Top and Bottom`); display([op(3..6,gra)],title=`Sides`);
![[Maple Plot]](plot3dexp/plot3dr_exp4.gif)
![[Maple Plot]](plot3dexp/plot3dr_exp5.gif)
![[Maple Plot]](plot3dexp/plot3dr_exp6.gif)
Solid with Six Pieces to its Boundary. (The Generic Elementary Region.)
Region in the first octant bounded above by z=x^2+y^2+1, below by z=0,
and on the sides by the xz plane, yz plane, the plane y=2 as well as the
parabolic cylinder x=(y-1)^2+1.
>
gr0:=plot3d_region(y=0..2,x=0..(y-1)^2+1,z=0..1+x^2+y^2,20):
display(gr0); display([gr0[1],gr0[2]],title=`Top and Bottom`); display([op(3..6,gr0)],title=`Sides`);
![[Maple Plot]](plot3dexp/plot3dr_exp7.gif)
![[Maple Plot]](plot3dexp/plot3dr_exp8.gif)
![[Maple Plot]](plot3dexp/plot3dr_exp9.gif)
Tetrahedron.
Solid Bounded by the planes x=0, y=0, z=0, 2x+y+3z=6.
>
gr5:=plot3d_region(x=0..3,y=0..6-2*x,z=0..(6-2*x-y)/3,20):
display(gr5); display([gr5[1],gr5[2]],title=`Top and Bottom`); display([op(3..6,gr5)],title=`Sides`);
![[Maple Plot]](plot3dexp/plot3dr_exp10.gif)
![[Maple Plot]](plot3dexp/plot3dr_exp11.gif)
![[Maple Plot]](plot3dexp/plot3dr_exp12.gif)
Between Two Paraboloids.
Solid Bounded by the paraboloids z=x^2+2y^2 and z=12-2*x^2-y^2.
>
gr6:=plot3d_region(x=-2..2,y=-sqrt(4-x^2)..sqrt(4-x^2),z=x^2+2*y^2..12-2*x^2-y^2,20):
display(gr6); display([gr6[1],gr6[2]],title=`Top and Bottom`); display([op(3..6,gr6)],title=`Sides`);
![[Maple Plot]](plot3dexp/plot3dr_exp13.gif)
![[Maple Plot]](plot3dexp/plot3dr_exp14.gif)
![[Maple Plot]](plot3dexp/plot3dr_exp15.gif)
>
Cylinder Cut By Some Planes.
Solid in the first octant cut off by the plane z=y and the cylinder 1=x^2+y^2.
>
gr2:=plot3d_region(x=0..1,y=0..sqrt(1-x^2),z=0..y,20):
display(gr2); display([gr2[1],gr2[2]],title=`Top and Bottom`); display([op(3..6,gr2)],title=`Sides`);
![[Maple Plot]](plot3dexp/plot3dr_exp16.gif)
![[Maple Plot]](plot3dexp/plot3dr_exp17.gif)
![[Maple Plot]](plot3dexp/plot3dr_exp18.gif)
Solid Bounded by Some Planes.
Solid Bounded by the planes x=0, y=0, z=0, y+z=1, x+z=1.
(Looking first at the graphs helps here.)
>
g2:=plot3d(1-x,x=0..2,y=0..2,color=red):
g3:=plot3d(1-y,x=0..2,y=0..2,color=blue):
display([g2,g3],axes=normal);
![[Maple Plot]](plot3dexp/plot3dr_exp19.gif)
Since the top of the solid is sometimes z=1-x and sometimes z=1-y, it is natural to use two pieces.
>
gr3:=plot3d_region(x=0..1,y=0..x,z=0..1-x,20):
gr4:=plot3d_region(x=0..1,y=x..1,z=0..1-y,20):
display([op(gr3),op(gr4)],title=`The Two Elementary Regions Combined`);
display(gr3); display([gr3[1],gr3[2]],title=`Top and Bottom`); display([op(3..6,gr3)],title=`Sides`);
gr4:=plot3d_region(x=0..1,y=x..1,z=0..1-y,20):
display(gr4); display([gr4[1],gr4[2]],title=`Top and Bottom`); display([op(3..6,gr4)],title=`Sides`);
![[Maple Plot]](plot3dexp/plot3dr_exp20.gif)
![[Maple Plot]](plot3dexp/plot3dr_exp21.gif)
![[Maple Plot]](plot3dexp/plot3dr_exp22.gif)
![[Maple Plot]](plot3dexp/plot3dr_exp23.gif)
![[Maple Plot]](plot3dexp/plot3dr_exp24.gif)
![[Maple Plot]](plot3dexp/plot3dr_exp25.gif)
![[Maple Plot]](plot3dexp/plot3dr_exp26.gif)
Between Two Parabolic Cylinders
The Solid Bounded Above by z=1-x^2 and Below by z=y^2.
(Looking first at the graphs helps here.)
>
g0:=plot3d(1-x^2,x=-2..2,y=-2..2,color=red):
g1:=plot3d(y^2,x=-2..2,y=-2..2,color=blue):
display([g0,g1],axes=normal);
![[Maple Plot]](plot3dexp/plot3dr_exp27.gif)
>
gr1:=plot3d_region(x=-1..1,y=-sqrt(1-x^2)..sqrt(1-x^2),z=y^2..1-x^2,20):
display(gr1); display([gr1[1],gr1[2]],title=`Top and Bottom`); display([op(3..6,gr1)],title=`Sides`);
![[Maple Plot]](plot3dexp/plot3dr_exp28.gif)
![[Maple Plot]](plot3dexp/plot3dr_exp29.gif)
![[Maple Plot]](plot3dexp/plot3dr_exp30.gif)
>