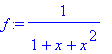
Taylor Series Experimentation
> with(plots):
Warning, the name changecoords has been redefined
One Variable Case
Taylor polynomials of degrees 1 through 4 for f about x=1.
>
f:=1/(1+x+x^2);
gr0:=plot(f,x=-2..2):
for i from 1 to 5 do
f || i:=mtaylor(f,[x=1],i+1);
od;
![]()
![]()
![]()
![]()
![]()
The first graph compares f with these Taylor polynomials for x between 0 and 2.
The second between -2 and 2.
Do you see a difference in the quality of the approximation?
What do you think would happen over [-2,2] with higher degree polynomials?
Would they eventually give a good approximation on the interval [-2,2]?
>
colors:=[red,yellow,green,blue,violet]:
gr0:=plot(f,x=-2..2,color=colors[1]):
for i from 1 to 4 do
gr || i := plot(f || i,x=-2..2,color=colors[i+1]):
od:
display([gr0,gr1,gr2,gr3,gr4],thickness=2,title=`Taylor polynomials about x=1; f is in red`,view=[0 .. 2,0..1]);
display([gr0,gr1,gr2,gr3,gr4],thickness=2,title=`Taylor polynomials about x=1; f is in red`);
![[Maple Plot]](taylorexp/Taylorexp7.gif)
![[Maple Plot]](taylorexp/Taylorexp8.gif)
>
A Basic Two Variable Example
The 3 below in the mtaylor call below means degree 3-1=2 Taylor polynomial .
>
g:=1/(y^2+x);
g2:=mtaylor(g,[x=1,y=1],3);
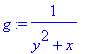
![]()
The first graph shows g and its second Taylor polynomial over the x_range and y_range specified.
The second graphs the difference, which may be interpreted as an error.
Try rotating the graphs (especially the first) to examine the quality of the approximation.
Try some other ranges besides the 0.5 .. 1.5 specified below.
Try at least some ranges close to 1 (e.g 0.9 .. 1.1 or 0.75 .. 1.25)
as well as some bigger ranges (e.g. 0 ..2 or 0.25 .. 1.75).
Use the second graph to compare maximal errors with the width of the x_range.
(e.g. compare the largest errors in the cases 0.9 .. 1.1 and 0.95..1.05)
How much smaller has the error become as the width of the interval halved?
Can you explain approximately why this is so?
Do bigger intervals also work this way when their size is halved?
>
x_range:=0.5 .. 1.5;
y_range:=x_range;
gr5:=plot3d(g,x=x_range,y=y_range,color=blue):
gr6:=plot3d(g2,x=x_range,y=y_range,color=red):
display([gr5,gr6],axes=normal,title=`g is in blue,p2 in red`);
plot3d(g-g2,x=x_range,y=y_range,axes=normal,title=`error using p2`);
![]()
![]()
![[Maple Plot]](taylorexp/Taylorexp13.gif)
![[Maple Plot]](taylorexp/Taylorexp14.gif)
Do you see something fundamentally different about the approximation on
a big range vs. a small one? You could try changing the degree of the Taylor
approximation above.
>
>