PDE's and Change of Variables
First order example from class.
This verifies that a function f(x,y) =g(x^2+y^2)
solves the PDE y f_x - x f_y = 0.
> expression := y*diff(f(x,y),x) - x*diff(f(x,y),y);
> subs(f(x,y) = g(x^2+y^2),expression);
![]()
![]()
The wave equation
We want to look at the change of variables u =x+y, v=x-y in this equation.
> waveqn := diff(f(x,y),x,x) - diff(f(x,y),y,y) = 0;
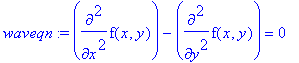
This means that f(x,y) = g(u,v) = g(x+y,x-y).
Without the simplify, this doesn't really give us what we want.
> waveqn2 := subs(f(x,y)=g(x+y,x-y),waveqn);
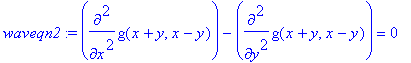
We see that the equation is of much simpler form now.
> waveqn2 := simplify(subs(f(x,y)=g(x+y,x-y),waveqn));
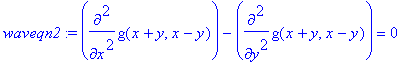
Now we express the new equation entirely in terms of u and v.
> invtrans := solve({u=x+y,v=x-y},{x,y});
![]()
The new equation is g_uv = 0.
(In general we might need more sophisticated simplification at this stage.)
> waveqn3 := subs(invtrans,waveqn2);
![]()
Laplace's equation in Polar Coordinates
Laplace's equation in two variables is given by
> lapeqn := diff(f(x,y),x,x) + diff(f(x,y),y,y)=0;
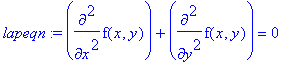
It is useful in applications to rewrite this equation in polar coordinates. To this end we set
> lapeqn2 := simplify(subs(f(x,y) = g(sqrt(x^2 + y^2),arctan(y/x)),lapeqn));
This doesn't look very simplified! Let's try coverting x and y into polar coordinates:
![]()
![]()
(sqrt(x^2+y^2),arctan(y/x))*x^2+...](pdechange/PDE_Change11.gif)
> lapeqn3 := simplify(subs(x=r*cos(theta),y=r*sin(theta),lapeqn2));
![]()
![]()
![]()
Ok, we're getting somewhere. However, there's still that annoying "csgn(r)" that arises because the square root of r*r is
|r| rather than just r. We know that r can be taken positive in polar coordinates, but Maple doesn't. Furthermore,
we see easily that
arctan(sin(theta)/cos(theta)) = arctan(tan(theta) = theta.
Maple misses that point--or seems to. Actually, Maple is probably only acting out of undue caution. In general,
arctan(tan(theta)) might be equal to "theta + k*pi" rather than just theta. In practice, we regard this sort of thing as
a technical point and ignore it until it gets us into trouble. Maple tends to avoid trouble at all costs. Rather than force Maple to see things our way,
we can just rewrite the equation by hand:
>
lapeqn4 := r^2 * diff(g(r,theta),r,r) +
r * diff(g(r,theta),r) +
r^(-2) * diff(g(r,theta),theta,theta) = 0;
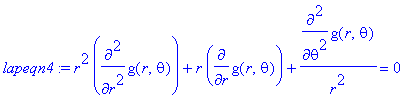
(Maple does have an assume facility that lets you announce things like "assume(r>0)" to get rid of the csgn, but there are real system limitations
on how far this gets you.
In general, harmonic functions (i.e. solutions of Laplace's equation) depend on r and theta, but it is interesting to see
if there are any harmonic functions h that depend on r alone.
> rlapeqn := simplify(subs(g(r,theta) = h(r),lapeqn4));
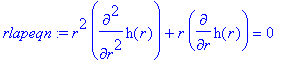
This is an ordinary differential equation with a simple solution.
> dsolve(rlapeqn,h(r));
![]()
The punchline is that any radially symmetric harmonic function is an affine function (i.e. linear function plus constant)
of log r.
Exercise: Laplace's equation in three variables is
>
laplace := diff(f(x,y,z),x,x) + diff(f(x,y,z),y,y)
+ diff(f(x,y,z),z,z) = 0;
Try turning this into an equation in spherical coordinates! What harmonic functions are functions of the radial variable
"rho" only?
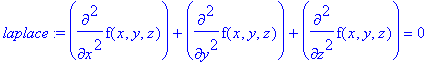
>
>