


Next: About this document ...
Up: Due in Recitation on
Previous: Markov Chain Models
The state data for 1980 in the table of regional population distribution above
could be entered in Maple using the commands:
with(linalg);
S[80] := vector(
[.2167,.2599, .1906, .3327 ] );
You can enter the data S[90] for 1990 similarly.
Let T be the 4 x 4 matrix
This problem will start out by testing the appropriateness of T as a
possible transition matrix describing regional population shifts over a decade.
- 1.
- By multiplying T on the left by the row vector [1,1,1,1], show that
the sums of the columns of T are close to 1. (Explain why multiplying by this row vector is calculating the column sum.)
- 2.
- Show that T approximately accounts for the change from 1980 to
1990, i.e.
![$T \circ S[80]$](img13.png) is approximately S[90].
is approximately S[90].
- 3.
- Compute
![$T^{50} \circ S[80]$](img14.png) ,
,
![$T^{100} \circ S[80]$](img15.png) ,
and
,
and
![$T^{200} \circ S[80]$](img16.png) ,
and compare these
results. What does the comparison suggest ?
,
and compare these
results. What does the comparison suggest ?
- 4.
- Use the row operations package to approximately solve the system
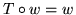 .
Explain why a state vector w satisfying this equation
would represent an unchanging (steady-state ) population
distribution for this model.
.
Explain why a state vector w satisfying this equation
would represent an unchanging (steady-state ) population
distribution for this model.
Maple Comments:
- Samples using the row operations package
are located in the file :Maple V Release 4:Math 221: Row
Operations Examples on each Macintosh in the Lab.
- To solve this system, you need only solve
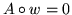 where
A is the matrix T-Id. The Maple commands
where
A is the matrix T-Id. The Maple commands
Id := diag(1,1,1,1);
A := T - Id;
will generate these matrices.
- A single use of the row operations package to solve
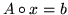 will include a read statement to load the package, a definition
of A and b, a ``start_ge(A,b);'' call, and then a sequence of
row operations (ar, mr and sr) as well as a
back-substitution (bs()). For decimals, one can use
(rounded_bs(k)) to round to k decimal places, thereby
rounding small entries (from roundoff error) to zero.
will include a read statement to load the package, a definition
of A and b, a ``start_ge(A,b);'' call, and then a sequence of
row operations (ar, mr and sr) as well as a
back-substitution (bs()). For decimals, one can use
(rounded_bs(k)) to round to k decimal places, thereby
rounding small entries (from roundoff error) to zero.
- Note also, that in using the row operations
package, you don't have to do arithmetic -- you can issue commands like:
ar(1,2, .7865/.2345);
- By approximately solve, we mean just work to 4 digit accuracy in your
row operations, and assume that naturally arising terms near 0 differ from
0 only because of roundoff error.
- There is a mathematically delicate issue associated with rounding here. The
square system (T - Id)w=0 is solvable nontrivially only
if T-Id is a singular matrix.
Doing row operations with floating point may change this into a matrix
that is non-singular although ``almost'' singular. A rigorous theory of
when and how to replace an almost singular matrix by a singular one is
somewhat difficult. Here we encourage you to just informally assume nearly
zero entries are really zero. But this will only work if you do not
unnaturally scale the entries.
For example if you have a row every entry of which is 0 except for
0.00001, then rounding to 4 decimal places will round all entries to 0.
But multiplying the row by 105 to make this nonzero entry 1 would
defeat the purpose of rounding.
- 5.
- Compare your steady state answer to the result of
![$T^{100} \circ S[80]$](img15.png) above. In converting your solution to one the sum of
whose components is 1, you may find it helpful to use
the Maple commands
above. In converting your solution to one the sum of
whose components is 1, you may find it helpful to use
the Maple commands
v_sum := add(v[i],i=1..4);
if v is a vector or
v_sum := add(v[i,1],i=1..4);
if v is a 4 x 1 matrix
to add up the 4 components of v and
mult := u -> u/v_sum;
map(mult,v);
The latter define a helper function multiplying any number by 1/v_sum, and then apply that
function to each entry of v.
The transition matrix T is just one Markov chain model consistent with the data. You
might find it interesting to think about other possibilities.
The fact that 3 and 4 agree can be shown
to hold in
general for Markov
matrices as long as some power has all its entries strictly positive.
But it's not obvious ....



Next: About this document ...
Up: Due in Recitation on
Previous: Markov Chain Models
root
2002-08-21

