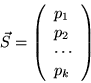
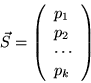
The state vector ![]() will depend on time t. In a discrete model,
we might measure the population fractions pi at times
will depend on time t. In a discrete model,
we might measure the population fractions pi at times
![]() .
Use
.
Use ![]() and pi[tn] respectively to denote values at the end of the n'th time period.
and pi[tn] respectively to denote values at the end of the n'th time period.
In a Markov chain model one assumes that there are transition probabilities Tij representing the proportion of the population in sub-population j during time period n which enter sub-population i for time period n+1. These transition probabilities are independent of time. Let T be the k x k matrix whose i,j entry is Tij.
We also assume that the entire population in time period n+1 comes by this
transition process from the population during time period n. Thus
More generally, we can keep track of the change in population over r time
periods by computing the r'th power of T. Specifically
![]() .
.
The sum of the entries in each column (e.g. the j'th) of the transition matrix T should be 1 because the entries of that column reflect all the possible destinations at time tn+1 for the people in region j at time tn.