


Next: Dirichlet Kernels
Up: Computation of the functions
Previous: Graphs of functions
The discrete inner products of the eigenfunctions are related to each
other. Let 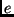 and
and 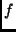 be eigenfunctions of
be eigenfunctions of 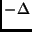 on the Sierpinski Gasket.
Pick a positive integer
on the Sierpinski Gasket.
Pick a positive integer 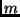 . Then the restrictions of
. Then the restrictions of 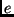 and
and 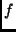 to
to 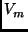 are
eigenfunctions of
are
eigenfunctions of 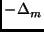 with some eigenvalue
with some eigenvalue 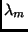 . We found that:
. We found that:
One Consequence of this is that a set eigenfunctions of 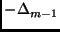 which is orthogonal at
level
which is orthogonal at
level 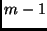 is also orthogonal at level
is also orthogonal at level 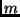 when extended by spectral decimation.
when extended by spectral decimation.
Since
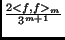 is a Riemann sum approximation for the integral over the
Sierpinski Gasket of
is a Riemann sum approximation for the integral over the
Sierpinski Gasket of 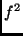 , this relation gives us:
, this relation gives us:
As you can see from the figure:
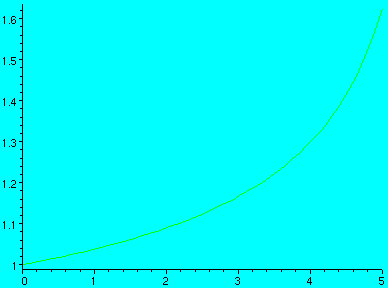
the correction factor
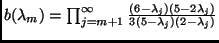 goes to
goes to 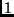 as
as 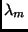 goes to
goes to 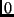 . (Calculation of the correction factor assumes that
subsequent eigenvalues are calculated with
. (Calculation of the correction factor assumes that
subsequent eigenvalues are calculated with 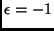 unless
unless  in which case the first
in which case the first 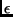 equals
equals 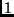 .)
.)
Brain Street
2001-11-11
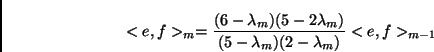
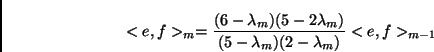
![]() is a Riemann sum approximation for the integral over the
Sierpinski Gasket of
is a Riemann sum approximation for the integral over the
Sierpinski Gasket of ![]() , this relation gives us:
, this relation gives us:
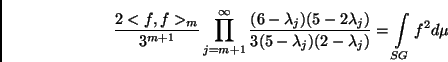

![]() goes to
goes to ![]() as
as ![]() goes to
goes to ![]() . (Calculation of the correction factor assumes that
subsequent eigenvalues are calculated with
. (Calculation of the correction factor assumes that
subsequent eigenvalues are calculated with ![]() unless
unless ![]() in which case the first
in which case the first ![]() equals
equals ![]() .)
.)