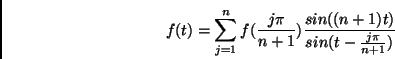Next: Computation of the functions
Up: sampling
Previous: sampling
Sampling is the practice of reconstructing a function from its values at a finite number of points. The simplest case is to
consider is a function
![$f:[0,\pi]\rightarrow\mathbb{R}$](img2.png) . Clearly, not every function can be reconstructed, as seen in the example below:
. Clearly, not every function can be reconstructed, as seen in the example below:
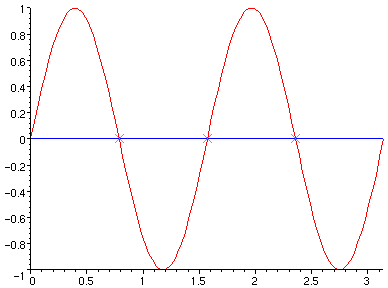
One will note that at the marked points, both the red and the blue functions
are 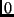 , but only one is the constant function
, but only one is the constant function 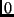 , hence sampling would fail at these points.
, hence sampling would fail at these points.
Hence, some restrictions must be put on 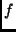 . For a sufficiently nice function
. For a sufficiently nice function 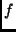 on
on ![$[0,\pi]$](img5.png) , with
, with 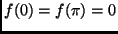 ,
, 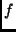 may be
expanded into a sine series:
may be
expanded into a sine series:
.
One says 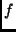 is band-limited with bandwidth
is band-limited with bandwidth 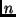 if
if
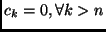 . In this case, one can see that in fact,
. In this case, one can see that in fact,
Hence, we see that bandlimited functions of bandwidth 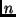 , can be reconstructed by sampling from
, can be reconstructed by sampling from 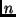 points.
points.
We wish to study the analogous concept on the Sierpinski Gasket. First, one must note
that
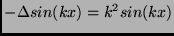 , and hence
, and hence 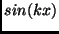 is an eigenfunction
of the laplacian of eigenvalue
is an eigenfunction
of the laplacian of eigenvalue 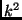 . Moreover,
. Moreover,
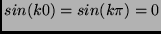 , and so
we say that
, and so
we say that 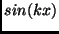 has Dirichlet boundary conditions. Hence, for a function
has Dirichlet boundary conditions. Hence, for a function  defined on the Sierpinski Gasket, we say
defined on the Sierpinski Gasket, we say  is bandlimited if
is bandlimited if
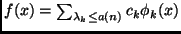 , where
, where
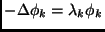 and
and
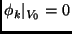 .
.
It makes the most sense to sample on 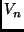 , the
, the 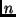 th level of the Sierpinski Gasket. One wishes to find functions
th level of the Sierpinski Gasket. One wishes to find functions
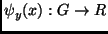 such that, for a band limited function
such that, for a band limited function 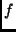 ,
,
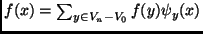 .
.
Hence, we wish to have
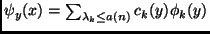 , and
, and
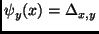 for
for 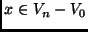 . Consider the matrix
. Consider the matrix
 , letting
, letting 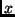 and
and 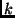 vary. This matrix is square and invertible due
to a result by Shima and Fukashima. Noting that
vary. This matrix is square and invertible due
to a result by Shima and Fukashima. Noting that 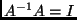 , we see that we
ought to define
, we see that we
ought to define
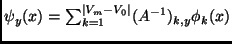 .
Since this was essentially a change of basis, clearly we will be able to
reconstruct bandlimited functions with these
.
Since this was essentially a change of basis, clearly we will be able to
reconstruct bandlimited functions with these 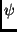 functions.
functions.



Next: Computation of the functions
Up: sampling
Previous: sampling
Brain Street
2001-11-11

![]() . For a sufficiently nice function
. For a sufficiently nice function ![]() on
on ![]() , with
, with ![]() ,
, ![]() may be
expanded into a sine series:
may be
expanded into a sine series: