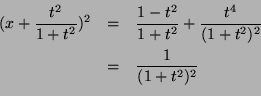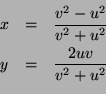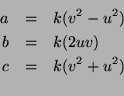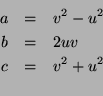Next: About this document ...
Pythagorean Triplets
ab
We seek to identify all positive integers a, b, and c so that
a2+b2=c2. A triple (a,b,c) satisfying this equation is
called a pythagorean triplet. Since any multiple
of a pythagorean triplet is again one, we only seek
primitive ones where a, b, and c have no common factor.
By setting 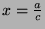 and
and 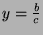 ,
we can first seek
rational numbers x and y so that x2+y2=1.
=2in
Now, if (x,y) is such a pair of rational
numbers, the line from (x,y) to (-1,0) will have rational
slope - call it t. Along this line, y=t(x+1), so
x2 +
t2(x+1)2=1 telling us that
,
we can first seek
rational numbers x and y so that x2+y2=1.
=2in
Now, if (x,y) is such a pair of rational
numbers, the line from (x,y) to (-1,0) will have rational
slope - call it t. Along this line, y=t(x+1), so
x2 +
t2(x+1)2=1 telling us that
(1+t2)x2 + 2t2 x = 1-t2
or
Complete the square on the above equation giving
Taking square roots gives
Write 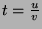 with u, v positive integers having no common
factor. This gives
with u, v positive integers having no common
factor. This gives
Using 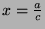 and
and 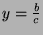 we see that
we see that
for some rational number k.
By thinking about the highest power pr of
an odd prime appearing in the denominator of k (written in lowest terms),
one sees that pr divides uv, u2+v2, -u2+v2, 2u2, and 2v2.
This means
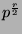 divides both u and v contradicting u
and v having no common factor, UNLESS r=0. Similarly by
noting exactly one of a and b can be odd, and choosing b to
be the even number, we can eliminate powers of 2 in
the denominator of k. This shows that k is
a whole number and we obtain:
Theorem: The pythagorean triplets with b even
are exactly the triples of the form
divides both u and v contradicting u
and v having no common factor, UNLESS r=0. Similarly by
noting exactly one of a and b can be odd, and choosing b to
be the even number, we can eliminate powers of 2 in
the denominator of k. This shows that k is
a whole number and we obtain:
Theorem: The pythagorean triplets with b even
are exactly the triples of the form
where u and v are positive whole numbers with no common factor.



Next: About this document ...
root
2002-09-26