Let
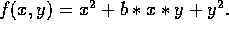Using Maple, for 
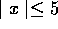and 
,
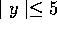plot the gradients of f for
b=1, 2, and 4. Print these out. On each of these printouts, draw in by hand
(roughly) several level curves.
Problem 1
Let 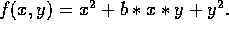Using Maple, for
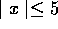and ,
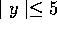plot the gradients of f for
b=1, 2, and 4. Print these out. On each of these printouts, draw in by hand
(roughly) several level curves.
Problem 2
We can consider the derivative Df of a function f at a point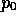 
as
an approximation of f
by an affine linear function. (The word affine here refers to the fact that
these approximations have constant terms in them.) Here we explore this
linear approximation
aspect of the derivative.
Consider the function
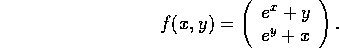
The corresponding first order approximation to f at the point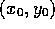 
is
given by
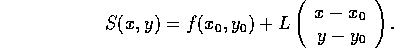
where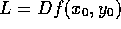 
is the derivative of f at the point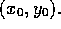 
Let C be a square of side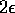 
centered at the point 
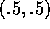, i.e.
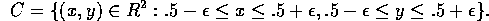
For 
taking on each ofthe values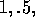 
and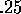 
, do the
following:
.
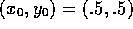For each value of 
, how do the images of C compare ?
What appears to be hapening as 
decreases?
The Maple procedure transform_rect available in the Math 222 folders will be useful here. The output of transform_rect is a Maple graphics structure, so you can assign the result to a variable and then display several of these simultaneously.