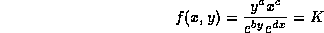
Use Maple for much of this problem.
Under the Volterra model of predator prey interaction, we will show later in the course that the population x of prey and y of predators (each a function of time t) are related by
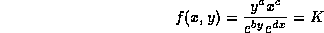
for suitable positive constants a, b, c, and d.
Suppose that 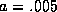 ,
, 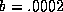 ,
, 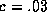 , and
, and 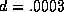 and that
at some time
and that
at some time 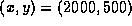 .
.
a) Find a value of the constant K so that the model 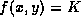 fits this data. (The Maple command
fits this data. (The Maple command
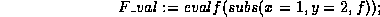
will evaluate an expression f at the point 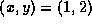 .)
.)
b) Use Maple to compute the partial derivatives of f at the
point 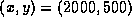 . (Recall that the Maple command
. (Recall that the Maple command

computes the partial derivatives symbolically.)
c)
Linear approximation along the level curve 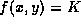 says that
says that
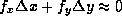 . We can solve this equation to
estimate y in terms of x near the point
. We can solve this equation to
estimate y in terms of x near the point 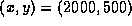 on the level curve. Use this technique to estimate the predator
population y as
on the level curve. Use this technique to estimate the predator
population y as 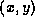 changes from
changes from 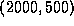 to x=1900.
to x=1900.
d) Use the Maple fsolve command to more exactly solve for the value of y that corresponds to x=1900. How do you explain the discrepancy from your answer in part c)? (The Maple command
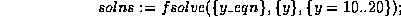
will look numerically for solutions to 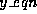 in the range y
between 10 and 20. For example
in the range y
between 10 and 20. For example 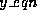 might be given by
might be given by
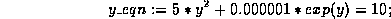
If no value is returned by Maple , this may mean there is no solution in this range, or it may mean that the solution method failed to converge.
e)
Use implicit differentiation to calculate
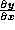 when
when
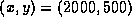 .
.
f) Repeat parts c) and d) using x=1999 instead of x=1900. Compare the quality of the linear approximation.