


Next: About this document
Up: No Title
Previous: No Title
Due on Friday, October 13.
Problem 1
A model for the motion of a moon around a planet is given by the curve
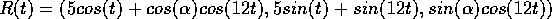
where 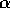 is the angle
is the angle 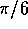 .
Plot a picture of the curve between 0 and
.
Plot a picture of the curve between 0 and 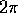 .
Plot a picture of the speed s(t) against t. From the picture estimate:
.
Plot a picture of the speed s(t) against t. From the picture estimate:
- a)
- The maximum and minimum speed of the particle between t=0 and
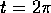 .
.
- b)
- All times between t=1 and t=2 when the particle will have a speed of 10.
Plot the length of the acceleration 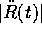 . From the picture
estimate the magnitudes of the maximal and minimal acceleration between t=0 and
. From the picture
estimate the magnitudes of the maximal and minimal acceleration between t=0 and 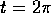 .
.
Problem 2
Let 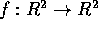 be defined by
be defined by
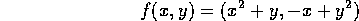
- a)
- Calculate the derivative of f at the point (1,-1).
- b)
- Write down the linear approximation g(x,y) to f(x,y)
at the point (1,-1). (So
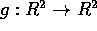 is an affine linear
function whose value and derivative agree with f at (1,-1).
is an affine linear
function whose value and derivative agree with f at (1,-1).
- c)
- Now view f and g as vector fields. Use the
Diffeq,Phase Plane program in MacMath to plot a
number of integral curves for each of these vector fields in
the region
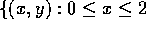 and
and 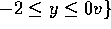 .
.
- d)
- Discuss how the two pictures compare.
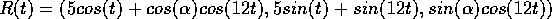



 is the angle
is the angle 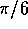 .
Plot a picture of the curve between 0 and
.
Plot a picture of the curve between 0 and 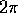 .
Plot a picture of the speed s(t) against t. From the picture estimate:
.
Plot a picture of the speed s(t) against t. From the picture estimate:
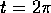 .
.
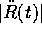 . From the picture
estimate the magnitudes of the maximal and minimal acceleration between t=0 and
. From the picture
estimate the magnitudes of the maximal and minimal acceleration between t=0 and 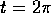 .
.
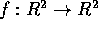 be defined by
be defined by
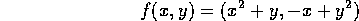
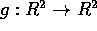 is an affine linear
function whose value and derivative agree with f at (1,-1).
is an affine linear
function whose value and derivative agree with f at (1,-1).
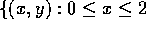 and
and 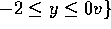 .
.