


Next: About this document
Up: No Title
Previous: No Title
You need only hand in question 1 and one of questions 2 and 3 on this
handout. (For extra credit you may hand in both of these.)
Problem 1
This problem deals with least squares fitting of the function
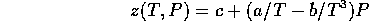
where a,b, and c are constants.
- a)
- Using Maple, derive formulas for the least squares
approximation of this function to a set of data

Recall that this involves the steps:
- Enter an expression for the total square error.
- Differentiate this with respect to a,b, and c.
- Solve the equations determining a critical point
for the variables a,b, and c.
Use our sample least squares worksheet as a reference here.
- b)
- The file :Math 222:lib:Ammonia Data inside the
Maple folders in the lab contains contains a table of data for
Ammonia.
The format is three numbers per line. The first entry is a
temperature T, the second a pressure P, and the third a
compressibility factor z. Use your formula from part a) to
estimate a,b, and c from the data file.
Here z is the compressibility factor (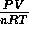 ), T is the
temperature and P is the pressure. (Thus for an ideal gas, z would just
be 1.) This formula is known as Berthelot's approximation to the
equation of state.
), T is the
temperature and P is the pressure. (Thus for an ideal gas, z would just
be 1.) This formula is known as Berthelot's approximation to the
equation of state.
Problem 2
Let 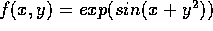 .
.
- a)
- Using the Maple function mtaylor, calculate
the Taylor series
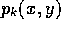 of orders k=1,2, and 4 about
of orders k=1,2, and 4 about
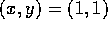 .
.
- b)
- By using Maple's plot3d command for the
function
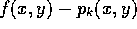 , estimate the maximum error in replacing
the function f by each of these Taylor polynomials in the region
, estimate the maximum error in replacing
the function f by each of these Taylor polynomials in the region
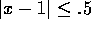 and
and 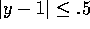 .
.
- c
- ) Similarly estimate the maximum error in replacing
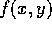 by
by 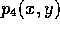 in the region
in the region 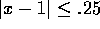 and
and
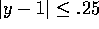 .
.
Problem 3
Let 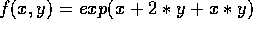
- a)
- Using Maple (or by hand) , calculate the Taylor
series of
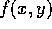 to order 2 about
to order 2 about 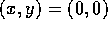 .
.
- b)
- Use plot3d in Maple to estimate the maximum
values of all third partial derivatives of
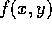 for
the region
for
the region 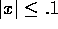 and
and 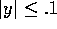 .
.
- c)
- Use the results of b) to find a reasonable
estimate of how big L can be so that the quadratic approximation
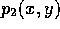 approximates
approximates 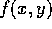 within .000001 for the region
within .000001 for the region
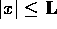 and
and 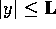 .
.



Next: About this document
Up: No Title
Previous: No Title
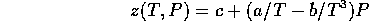



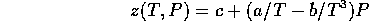

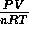 ), T is the
temperature and P is the pressure. (Thus for an ideal gas, z would just
be 1.) This formula is known as Berthelot's approximation to the
equation of state.
), T is the
temperature and P is the pressure. (Thus for an ideal gas, z would just
be 1.) This formula is known as Berthelot's approximation to the
equation of state.
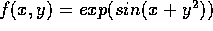 .
.
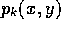 of orders k=1,2, and 4 about
of orders k=1,2, and 4 about
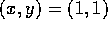 .
.
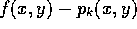 , estimate the maximum error in replacing
the function f by each of these Taylor polynomials in the region
, estimate the maximum error in replacing
the function f by each of these Taylor polynomials in the region
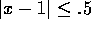 and
and 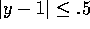 .
.
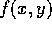 by
by 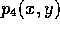 in the region
in the region 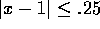 and
and
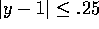 .
.
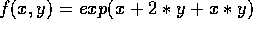
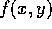 to order 2 about
to order 2 about 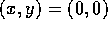 .
.
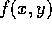 for
the region
for
the region 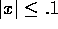 and
and 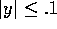 .
.
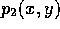 approximates
approximates 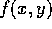 within .000001 for the region
within .000001 for the region
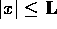 and
and 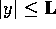 .
.


