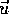Handout 7

Due Friday October 27.

Problem 1

This problem explores the relationship between local extrema of functions and the geometry of flowlines for their gradients.

a)

Compute the gradient vector field of the quadratic function

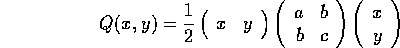
associated with the symmetric matrix

b)

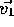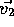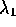Let and be orthogonal unit eigenvectors of A with respective eigenvalues and 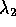. Verify that

is an integral curve for the gradient vector field 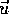. (It is a fact from linear algebra that because A is symmetric, the eigenvalues of A will always be real, and the eigenvectors corresponding to different eigenvalues may be chosen to be orthogonal.)

c)

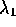When the eigenvalues and 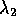are both nonzero with (say) 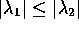there are five cases:

Improper Node Source:

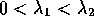
Proper Node Source:

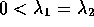
Saddle Equilibrium:

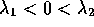(Here the relative magnitudes of 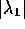and 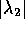are not qualitatively very significant.)

Improper Node Sink:

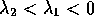
Proper Node Sink:

For each of these:

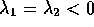
1. Give an example of a symmetric matrix whose eigenvalues satisfy the stated conditions.
2. Decide what kind of critical point (local minimum, local maximum, or saddle) the origin 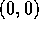is for the function .
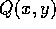3. Using MacMath's phase plane program, plot some flowlines for the gradient vector field 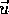in this case. Write a brief paragraph describing the geometry that you see. You can discuss factors such as where the solutions tend to approach in forward and backward time, as well as the directions most solutions tend to follow for large positive or negative time.

Problem 2

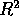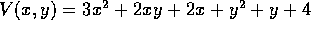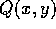Read section 4.5 of Marsden and do (without a computer) Marsden page 297 number 1. This talks about a particle moving in a potential field on given by . ( The in problem 1 is an example ( with a change in sign ) of the kind of potential 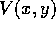discussed in that section. )