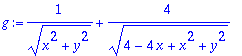
Gravitational Field Experiment
>
with(plots):
with(linalg):
Warning, the name changecoords has been redefined
Warning, the protected names norm and trace have been redefined and unprotected
Two body case.
> g:=1*(1/sqrt(x^2+y^2)+4/sqrt((2-x)^2+y^2));
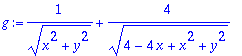
Two Dimensional Gravitational Potential for three body problem.
Unit mass at (0,0) and (1,1). Mass 4 at (2,0).
> f:=1*(1/sqrt(x^2+y^2)+4/sqrt((2-x)^2+y^2))+1/sqrt((1-x)^2+(1-y)^2);
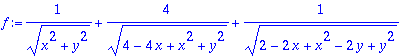
After you execute this worksheet (including the with(plots) line above),
below will be the level curves of f for the values 2 and 10.
You can add other comma separated values for f between 2 and 10 to see more level sets.
What happens in between 2 and 10?
Are there values when the level sets change their shape?
If so can you find them? Accurately?
What happens to the level sets of the function g?
> contourplot(f,x=-4..5,y=-4..4,grid=[100,100],contours=[2,10],coloring=[red,blue],thickness=2);
>
>