
This portion involves using the program Surfaces to plot some surfaces.
Please hand the answers to these questions in by the time of your lab recitation next week (i.e. Wednesday afternoon 9/11 or Thursday morning 9/12.)
Support your answers by rough sketches of what you see in the computer program. The program Surfaces does not print very well (and a lot of paper would be consumed ...), so please do not print a large number of examples.
Problem 1 Look at the graph of

for values of c positive, negative, and zero.
What kinds of quadric surfaces do you see for this range of c values?
Find the critical values of c when the shape of these quadric surfaces changes.
What happens to the shape of these quadric surfaces as the absolute value of c increases?
Problem 2 Look at the graph of

for values of c positive, negative, and zero.
What kind of quadric surface do you see when  is large?
is large?
How about when c is small in absolute value?
Estimate the critical values of c when the qualitative nature of these quadric surfaces appears to change.
What does the graph look like for these values of c?
Problem 3 Consider the graphs of

and

for the the values 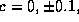 or
or 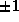 .
.
What quadrics do you get for each of these values of c?
Relate what you see to the following statement:
``A cone can be a borderline case between a one and two sheeted hyperboloid.''