Let
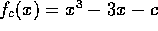 . When c=2,
. When c=2,
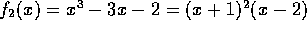 . This problem studies the behavior
of solutions of
. This problem studies the behavior
of solutions of 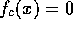 as a function of the parameter c. Let
as a function of the parameter c. Let
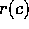 be the function of c whose value is the smallest root of
this polynomial. For example
be the function of c whose value is the smallest root of
this polynomial. For example 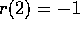 since -1 is the smallest
root of
since -1 is the smallest
root of 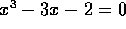 .
.
Problem 1
Let 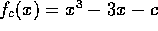 . When c=2,
. When c=2,
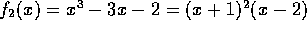 . This problem studies the behavior
of solutions of
. This problem studies the behavior
of solutions of 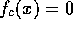 as a function of the parameter c. Let
as a function of the parameter c. Let
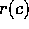 be the function of c whose value is the smallest root of
this polynomial. For example
be the function of c whose value is the smallest root of
this polynomial. For example 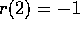 since -1 is the smallest
root of
since -1 is the smallest
root of 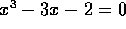 .
.
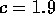 and
and 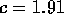 , find the smallest
root of
, find the smallest
root of 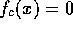 . Use these values to estimate
. Use these values to estimate 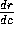 when
when 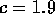 . (Note that the Maple
. (Note that the Maple
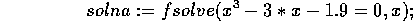
will generate an expression sequence of three roots and they can be referred to as solna[1],solna[2], and solna[3].
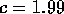 and
and 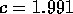 , and use these to estimate
, and use these to estimate 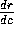 when
when 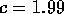
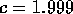 and
and 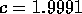 , and use these to estimate
, and use these to estimate 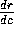 when
when 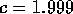
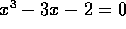 appear to be
a differentiable function of c when c=2? Explain !
appear to be
a differentiable function of c when c=2? Explain !
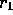 and
and 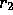 , the cubic
equation
, the cubic
equation
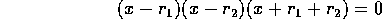
is of the form

where
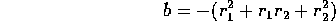
and

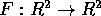 by
by
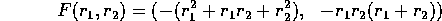
Calculate the derivative of F.
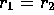 .
.
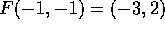 . Show using part g)
that F does not have a differentiable local inverse G
satisfying
. Show using part g)
that F does not have a differentiable local inverse G
satisfying  . Relate this to your answer in part
d).
. Relate this to your answer in part
d).
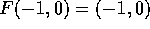 . Show that F does have a
differentiable local inverse G
satisfying
. Show that F does have a
differentiable local inverse G
satisfying 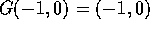 .
.
Don't feel obliged to use the computer for each part above.
To ease the calculations, the above problem looked at the dependence
of roots upon coefficients for cubic equations with no 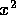 term.
The (possible) local inverses G above are functions describing
two of the roots as a function of the two nonzero coefficients.
Part h) was looking at a typical case near where two roots were
equal, while in part i), all roots were distinct.
term.
The (possible) local inverses G above are functions describing
two of the roots as a function of the two nonzero coefficients.
Part h) was looking at a typical case near where two roots were
equal, while in part i), all roots were distinct.
By multiplying out 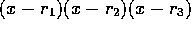 , and defining an appropriate
, and defining an appropriate 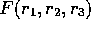 , one can similarly analyze the roots of a
general cubic equation as a function of all three coefficients.
, one can similarly analyze the roots of a
general cubic equation as a function of all three coefficients.