


Next: About this document ...
Up: Math 221 Fall 98
Previous: Some Matrices and Parallelograms
As you do the following questions, we'd like you to look at a fair
number of results of
gr1 := pargrm_image_2d([vi,vj],Ak);
display(gr1, scaling=constrained);
but don't print them all. Also note that once you have two lines
like the above in your Maple session, you can just edit the indices
i,j,k and then hit ENTER again to see the next set of
pictures.
In these questions, some parts involve looking at a computer result,
while others involve a mathematical argument. We'll use the symbol
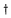 to indicate questions whose answers are primarily of a computer
nature and
to indicate questions whose answers are primarily of a computer
nature and  for questions requesting other arguments. Some parts
of the questions, are providing defintions and explanations; you
don't need to answer those of course!
for questions requesting other arguments. Some parts
of the questions, are providing defintions and explanations; you
don't need to answer those of course!
- a)
- A square matrix
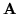 with the property that
with the property that 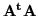 is
the identity is called orthogonal. Show
is
the identity is called orthogonal. Show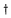 that
that 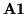 and
and 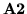 meet this
definition of orthogonality. (The importance of the definition
is that the associated linear transformations preserve distances and
angles.)
meet this
definition of orthogonality. (The importance of the definition
is that the associated linear transformations preserve distances and
angles.)
- b)
- Look
 at the result of transformation
at the result of transformation 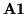 on the
four parallelograms above. A reflection of
on the
four parallelograms above. A reflection of 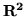 is an
orthogonal transformation
is an
orthogonal transformation 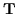 with the further property that it leaves one
nonzero vector
with the further property that it leaves one
nonzero vector 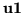 fixed (i.e.
fixed (i.e.
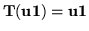 )
and reverses another
vector
)
and reverses another
vector 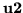 (i.e.
(i.e.
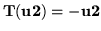 ). The vector
). The vector 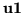 is called
the axis of the reflection. Print
is called
the axis of the reflection. Print out one picture suggesting
what the axis of
out one picture suggesting
what the axis of 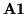 is likely to be. Then show
is likely to be. Then show algebraically that
vectors
algebraically that
vectors 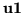 and
and 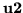 as above exist for
as above exist for 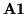 .
.
- c)
- Look
 at the result of transformation
at the result of transformation 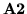 on the
four parallelograms above. Can you see why
on the
four parallelograms above. Can you see why the word rotation is
used to describe the action of A2 ? (To explain this, relate a picture to the
ordinary English meaning of the word.) Show
the word rotation is
used to describe the action of A2 ? (To explain this, relate a picture to the
ordinary English meaning of the word.) Show that
that 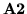 has no nonzero
fixed vectors, i.e.
has no nonzero
fixed vectors, i.e.
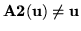 for all vectors
for all vectors
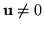 .
.
- d)
- It can be shown that all rotations are of the form
for some angle 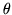 .
Show
.
Show that the matrices
that the matrices 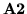 and
and 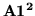 are
both rotations. (It is in fact true that the composition of two reflections is always a
rotation.)
are
both rotations. (It is in fact true that the composition of two reflections is always a
rotation.)
- e)
- Look
 at the result of transformation
at the result of transformation 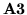 on the
four parallelograms above. A shear transformation of
on the
four parallelograms above. A shear transformation of 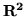 is a
linear transformation with the properties:
is a
linear transformation with the properties:
- 1.
- It leaves one nonzero vector
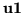 fixed
(i.e.
fixed
(i.e.
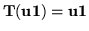 ). The vector
). The vector 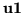 is the axis of
the shear.
is the axis of
the shear.
- 2.
- For any vector
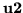 ,
the difference between
,
the difference between
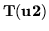 and
and 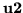 is parallel to the axis
is parallel to the axis 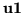 .
.
By looking at the results of the transformation 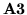 on the
four parallelograms above, find
on the
four parallelograms above, find the axis of the shear
the axis of the shear 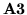 .
Also, show algebraically
.
Also, show algebraically that
that 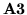 meets the definition
above of a shear transformation.
meets the definition
above of a shear transformation.
- f)
- Look
 at the result of linear transformation
at the result of linear transformation  on
parallelogram P2. Explain using the definition above
on
parallelogram P2. Explain using the definition above why this picture suggests
why this picture suggests  is a
shear. What is its axis (
is a
shear. What is its axis (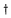 or
or  )?
)?
- g)
- Look
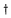 at the result of transformation
at the result of transformation 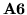 on the
four parallelograms above. A dilation is a linear transformation
preserving angles and directions, but not necessarily distances. Show
on the
four parallelograms above. A dilation is a linear transformation
preserving angles and directions, but not necessarily distances. Show for any two vectors
for any two vectors 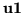 and
and 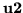 ,
the angle between them
is the same as the angle between their images
,
the angle between them
is the same as the angle between their images 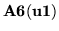 and
and 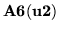
- h)
- Look
 at the result of transformation
at the result of transformation 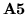 on
parallelogram P2. Give
on
parallelogram P2. Give a description of what you see in terms of
change of scale of the sides of P2. Does
a description of what you see in terms of
change of scale of the sides of P2. Does this change of scale
interpretation appear to hold for any of the other parallelograms ?
this change of scale
interpretation appear to hold for any of the other parallelograms ?
- i)
- Print
 out the result of transformation
out the result of transformation 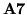 on one of these parallelograms, and explain
on one of these parallelograms, and explain the result.
the result.
One reason for talking about shears, dilations, and orthogonal
transformations is that any linear transformation of 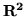 can be expressed as
a composition of one each of these together with one more basic
transformation, a strain. A typical strain would be given by the matrix
can be expressed as
a composition of one each of these together with one more basic
transformation, a strain. A typical strain would be given by the matrix
This also generalizes to higher dimensions.



Next: About this document ...
Up: Math 221 Fall 98
Previous: Some Matrices and Parallelograms
root
2002-08-21
![]() to indicate questions whose answers are primarily of a computer
nature and
to indicate questions whose answers are primarily of a computer
nature and ![]() for questions requesting other arguments. Some parts
of the questions, are providing defintions and explanations; you
don't need to answer those of course!
for questions requesting other arguments. Some parts
of the questions, are providing defintions and explanations; you
don't need to answer those of course!
![]() can be expressed as
a composition of one each of these together with one more basic
transformation, a strain. A typical strain would be given by the matrix
can be expressed as
a composition of one each of these together with one more basic
transformation, a strain. A typical strain would be given by the matrix