Regular Patterns

Let's try and understand patterns which repeat along an infinite strip. We want there to be a group of rigid motions taking the strip to itself as well as the pattern to itself. The group should include all multiples backwards and forwards of a particular translation. By choosing which way to orient and scale our coordinates, we can normalize the strip to be 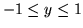$-1 \leq y \leq 1$ and the smallest translation 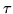$\tau$ to the right one unit; i.e. $\tau(x,y)=(x+1,y)$.

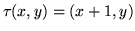It turns out there are only 7 essentially different symmetry groups which can arise this way ! The program Kali lets us pick one of these, draw a pattern and see what the symmetries do.

Let's try and understand how one can come up with a conclusion like this result that only 7 possibilities exist. As you think about some of the questions below, experiment with Kali to try and get some insight.