


Next: Numerical Integration
Up: Flowlines, Vector Fields, Numerical
Previous: Vector Fields and Flowlines
By appending a 0 z-component to
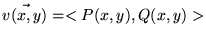 ,
we
can consider the vector field
,
we
can consider the vector field
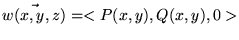 whose divergence is
whose divergence is
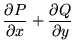 and whose curl is
and whose curl is
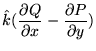 .
.
The folder :Maple V Release 4:Math 222:Lecture 5 contains
small movies of the flows associated to the four
vector fields given below. (The flow of a vector field on a set
at time t gives a new set representing where at time t the points
of the old set would be if each followed a flowline for time t.)
The four examples there are
- Nonzero Divergence and Zero Curl:
-
v(x,y)=<5x+10y,10x+5y>.
- Zero Divergence and Zero Curl:
-
v(x,y)=<5x+10y,10x-5y>.
- Zero Divergence and Nonzero Curl:
-
v(x,y)=<10y,-10x>.
- Nonzero Divergence and Zero Curl:
-
v(x,y)=<5x+15y,-10x+5y>.
For each of these, look at the vector fields and a few integral curves
in one of the MacMath programs mentioned above. Can you see a
relationship to the flows?
root
2002-08-23
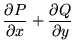 and whose curl is
and whose curl is
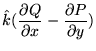 .
.