


Next: About this document ...
Some Conformal Mappings to Try in Complex Paint
With Complex Paint, you can draw in either the domain or the range. Also, the Equation menu lets you both change the mapping and adjust the domain and range. Try
- a)
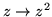 :
:
- First quadrant to the half space {Im(z) > 0}. The rectangular
grid tool might be especially useful here.
- b)
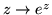 :
:
- The strip
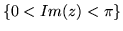 to the half space
{Im(z) > 0}.
to the half space
{Im(z) > 0}.
- c)
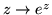 :
:
- The half-strip
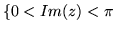 ,
Re(z) < 0}
to a half disk.
,
Re(z) < 0}
to a half disk.
- d)
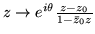 :
:
- The unit disk
to itself, z0 to 0. What is the geometric effect of the
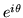 term?
What happens to a small circle around z0?
term?
What happens to a small circle around z0?
- e)
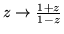 :
:
- Upper half of unit disk to first quadrant.
Check where the unit circle goes. How about the real axis? Compare the images of
the quadrant 2 portion of the unit disk and the quadrant 1 portion.
- f)
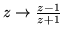 :
:
- Halfplane
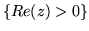 to unit disk.
Increasing the domain size will help here.
to unit disk.
Increasing the domain size will help here.
- g)
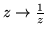 :
:
- The inside of the unit disk to its exterior.
- h)
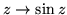 :
:
- The half strip
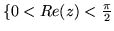 ,
Im(z) >0} .
,
Im(z) >0} .



Next: About this document ...
root
2002-08-23